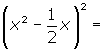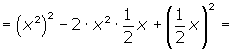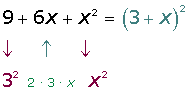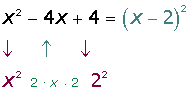SUMA Y RESTA DE POLINOMIOS
SUMA DE POLINOMIOS
Para sumar o restar polinomios, hay que sumar o restar entre sí los monomios que sean semejantes (misma parte literal)
Ejemplos: 2x+3x = 5x
(3x2+2x) + (4x2+3x) = 7x2+5x
si no hay términos semejantes, se deja indicado:
Ejemplo: 3x2+2xno son semejantes, se deja indicado
La suma o la resta de dos o más polinomios pueden realizarse sumando o restando sus términos semejantes. Estas operaciones pueden hacerse en vertical y en horizontal o en fila.
Para ello nos fijaremos en los siguientes polinomios: P(x) = 7x2 – 5x4 +3x – 15 y Q(x) = 5x3 – 7 + 9x2 – 6x
• En vertical: se ordenan los polinomios en orden decreciente y se disponen uno sobre el otro, de forma que en la misma columna se encuentren los términos semejantes:
P(x) = –5x4 + 0x3 + 7x2 + 3x – 15
Q(x) = 5x3 + 9x2 – 6x – 7
________________________________
–5x4 + 5x3 + 16x2 – 3x – 22
NOTA: En este caso es cuando todos los coeficientes son iguales lo único que hay que hacer es ordenarlos de mayor a menos de forma descendente, en caso de que tengas el mismo valor exponencial, ordenarlos por orden alfabético.
Posteriormente el maestro explicara este caso en la forma vertical y nos ejercicios con sus respectivas respuestas para que practiquen y así poder dominar la suma de polinomios y no equivocarse.
NOTA: Este caso es cuando el exponente mayor no tiene con quien simplificarse por que no tiene términos semejantes se deja un espacio vacío y pasa igual por lo tanto quedaría indicado.
a continuación el maestro explicara este caso en la forma vertical y unos ejercicios con sus respectivas respuestas para que practiquen y así poder dominar la suma de polinomios y no equivocarse.
–5x4 + 5x3 + 16x2 – 3x – 22
• En horizontal o en fila: se ordenan los polinomios, escritos entre paréntesis, en orden decreciente, uno a continuación del otro y separados por el símbolo de la operación; a continuación se suman o se restan los términos semejantes:
P(x) + Q(x) = (–5x4 + 0x3 + 7x2 + 3x – 15) + (5x3 + 9x2 – 6x – 7) =
= –5x4 + 5x3 + 16x2 – 3x – 22
P(x) – Q(x) = (–5x4 + 0x3 + 7x2 + 3x – 15) – (5x3 + 9x2 – 6x – 7) =
= –5x4 – 5x3 – 2x2 + 8x – 8
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
P(x) = 2x3 + 5x − 3 Q(x) = 4x − 3x2 + 2x3
1.- Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x) + Q(x) = (2x3 + 5x − 3) + (2x3 − 3x2 + 4x)
2.- Agrupamos los monomios del mismo grado.
P(x) + Q(x) = 2x3 + 2x3 − 3 x2 + 5x + 4x − 3
3.- Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3 − 3x2 + 9x − 3
También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.
P(x) = 7x4 + 4x2 + 7x + 2 Q(x) = 6x3 + 8x +3
P(x) + Q(x) = 7x4 + 6x3 + 4x2 + 15x + 5
Sumar polinomios
Un término es una expresión que está separada por los signos de suma o resta.
Ejemplos de términos: 3x , -2x2, 4
Ejemplo:
3x2 - 4x
3x2 es un término. -4x es otro término.
Un constante es un término que no contiene variables, solamente posee coeficiente.
3x2 + 9x + 8 En este caso, la constante es 8, ya que es el único término sin variables.
Un monomio es un número, una variable o un producto de números y variables.
Algunos ejemplos de monomios son:
3x 2, 2x, -5, 37
x No es un monomio porque la variable aparece en el denominador.
Un polinomio es una expresión cuyos términos son monomios.
x2 + 2x - 8
Un monomio es un polinomio con un término.
5x3 Es un monomio
Un binomio es un polinomio con dos términos.
5y2 - 3x es un binomio.
Un trinomio es un polinomio con tres términos.
6xy - 2r2s + 4r Es un trinomio.
Polinomios con más de tres términos no reciben nombres especiales..
Los términos de un polinomio en una variable se arreglan usualmente de modo que los exponentes de la variable van en orden de mayor a menor y de izquierda a derecha. Esto se llama orden descendente.
4x3 - 3x2 + 6x - 1
5y4 - 2y3 + y2 - 7y + 8
El grado de un polinomio es una variable es el exponente mayor.
El Polinomio de 4x3 -3x2 + 6x - 1 es de grado 3
5y4 - 2y3 + y2- 7y + 8 es un polinomio de grado 4.
Polinomios pueden ser sumados, usando un formato vertical, mediante la combinación de términos semejantes.
Por ejemplo simplifica (2x2 + x - 1) + ( 3x3 + 4x2 - 5 ) usando el formato vertical.
Primero los términos son arreglados.
En orden descendente son términos semejantes en la misma.
2x2 + x - 1
+ 3x3 + 4x2 - 5
3x3 + 6x2 + x -6
Simplifica (3x3 - 7x + 2) + ( 7x2 + 2x -7) usando el formato horizontal.
Pasos:
1).- Usando las propiedades conmutativas (3x3 - 7x + 2) + (7x2 + 2x -7)
y asociativas de la adición de reemplazar
los términos semejantes. 3x3 + 7x2 + (-7x + 2x) + (2 + -7)
(Este paso se hace mentalmente.)
2).- Combinar términos semejantes.
3).- Escribir el polinomio en orden descendente. 3x3 + 7x2 - 5x -5
Ejemplo 1:
Escribe el siguiente polinomio en orden descendente.
3x2 - 5 + 4x3 - 2x
Solución:
4x3 + 3x2 -2x -5
Nota: Fíjate que hemos reescrito 7y2 - 6y + 9 como 7y2 + -6y + 9 (usando las reglas de la resta - restar un número es igual que sumar el opuesto del número)
Simplifica ( -4x2 - 3xy + 2y 2 ) + ( 3x2 - 4 y2 ). Usar el formato horizontal. En este tipo de suma se agrupan horizontalmente los términos semejantes. Términos semejantes son aquellos que tienen la misma variable o variables con el mismo exponente.
Solución:
(- 4x2 - 3xy + 2y2) + (3x2 - 4y2)=
-4x2 + 3x2 + -3xy + 2y2 + -4y2
-x2 - 3xy - 2y2
Posteriormente el maestro explicara este caso en la forma horizontal.
Bueno a continuación un ejemplo más de suma de polinomios.
RESTA DE POLINOMIOS
Polinomios pueden ser restados usando el formato vertical o el formato horizontal. Recuerda que para restar es lo mismo sumar el opuesto del polinomio.
Simplifica ( -3x2 - 7) - (-8x2 + 3x + -4). Usa el formato vertical.
1. Arreglar los términos de cada polinomio en orden descendente con los términos semejantes en la misma columna.
2. Reescribes la resta como la suma del opuesto.
3. Combinar los términos en cada columna.
También podemos restar polinomios escribiendo el opuesto de uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.
P(x) = 7x4 + 4x2 + 7x + 2 Q(x) = 6x3 + 8x +3
7X4 +4X2+7X +2
-6X3 -8X -3
____________________________
7X4 - 6X3 +4X2 - X - 1
Posteriormente el maestro explicara este caso en la forma vertical y unos ejercicios con sus respectivas respuestas para que practiquen y así poder dominar la resta de polinomios y no equivocarse.
A continuacion un ejemplo más de resta de polinomios de la forma vertical.
Resta de polinomios
La resta de polinomios consiste en sumar el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x − 4x − 3
P(x) − Q(x) = 3x2 + x − 3
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
P(x) = 2x3 + 5x − 3 Q(x) = 4x − 3x2 + 2x3
1.- Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x) + Q(x) = (2x3 + 5x − 3) + (2x3 − 3x2 + 4x)
2.- Agrupamos los monomios del mismo grado.
P(x) + Q(x) = 2x3 + 2x3 − 3 x2 + 5x + 4x − 3
3.- Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3 − 3x2 + 9x − 3
También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.
P(x) = 7x4 + 4x2 + 7x + 2 Q(x) = 6x3 + 8x +3
P(x) + Q(x) = 7x4 + 6x3 + 4x2 + 15x + 5
Resta de polinomios
La resta de polinomios consiste en sumar el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x − 4x − 3
P(x) − Q(x) = 3x2 + x − 3
Posteriormente el maestro explicara este caso en la forma horizontal.
CONCLUSION
ANEXSO ESTO QUE ES MUY INPORTANTE SABERLOS LOS AXIOMAS Y FORMULAS DE SUMA Y RESTA DE POLINOMIOS APLICADOS.
Suma o adición de polinomios
Propiedades de la adición en el conjunto de polinomios
a) Ley de cierre
La suma de dos o más polinomios da un polinomio.
b) Propiedad asociativa
Hacer 1º p(x) más q(x) y luego sumarle r(x) es igual que hacer 1º q(x) más r(x) y sumarle p(x).
c) Existencia del elemento neutro
Si a p(x) le sumas 0 te sigue quedando p(x). Recordar que al polinomio 0 se lo denomina polinomio nulo.
d) Existencia del opuesto aditivo
Si a p(x) le sumas su opuesto, es decir,-p(x), te da 0.
e) Propiedad conmutativa
Decir p(x) más q(x) es lo mismo que decir q(x) más p(x).
Nota: Debe prestarse atención a la existencia del opuesto aditivo. Para obtener el opuesto aditivo de un polinomio basta con cambiar el signo de cada uno de sus términos.
Observar que el grado de la suma o adición de polinomios es igual o menor que el grado del polinomio sumando de mayor grado.
Resta o Sustracción de Polinomios
Propiedades de la resta de polinomios
Propiedad Asociativa.- Se hace primero p(x) más q(x) y luego restarle r(x) es igual que hacer primero q(x) más r(x) y restarle p(x).
Elemento Neutro.- Si a p(x) le restas 0 te sigue quedando p(x).
Elemento Opuesto.- Si a p(x) le restas su opuesto, es decir, + p(x), te da 0.
ESPERO AVER PODIDO RESOLVER TODAS SUS DUDAS ENSEGUIDA PONDRE UN EJEMPLO DE LAS DOS, SUMA Y RESTA DE POLINOMIOS.