Cuadrado de binomio
más el doble producto del primero por el segundo más el cuadrado segundo.
(a + b)2 = a2 + 2 · a · b + b2
Cuando un binomio se multiplica por sí mismo se tiene lo que se conoce como un binomio al cuadrado. Después de desarrollar la multiplicación se obtiene un trinomio cuadrado perfecto. Si para un binomio cualquiera consideramos el primer término como a y el segundo término como b, entonces el binomio es a + b y también podemos expresar el binomio al cuadrado como (a + b) 2. Si desarrollamos la multiplicación se tiene:
(a + b)2 = (a + b)(a + b)
(a + b)2 = aa + ab + ba + bb
(a + b)2 = a2 + 2ab + b2
(a + b)2 = aa + ab + ba + bb
(a + b)2 = a2 + 2ab + b2
sustituimos el valor de "a"
donde: a=3
(x + 3)2 = x 2 + 2 · x ·3 + 3 2
= x 2 + 6 x + 9
Usando la identidad se tiene que: (x + 2y)2 = (x)(x) + 2(x)(2y) + (2y)(2y)
(x + 2y)2 = x2 + 4xy + 4y2
(3xy + 5)2 = (3xy)(3xy) + 2(3xy)(5) + (5)(5)
(3xy + 5)2 = 9x2y2 + 30xy + 25
Binomio de resta al cuadrado
menos el doble producto del primero por el segundo, más el cuadrado segundo.
(a − b)2 = a2 − 2 · a · b + b2
Lo anterior nos indica que cuando los términos del binomio tienen signos opuestos, en el resultado el término del doble producto del primero por el segundo tiene signo negativo.
La identidad (a + b)2 = a2 + 2ab + b2 es válida para todos los binomios, pero se puede particularizar más para el caso de que los términos del binomio tengan signos diferentes, en ese caso, al elevar al cuadrado y desarrollar la multiplicación tenemos:
(a - b)2 = (a - b)(a - b)
(a - b)2 = aa + (a)(-b) + (-b)(a) + (-b)(-b)
(a - b)2 = aa - ab - ab + bb
(a - b)2 = a2 - 2ab + b2
La identidad (a + b)2 = a2 + 2ab + b2 es válida para todos los binomios, pero se puede particularizar más para el caso de que los términos del binomio tengan signos diferentes, en ese caso, al elevar al cuadrado y desarrollar la multiplicación tenemos:
(a - b)2 = (a - b)(a - b)
(a - b)2 = aa + (a)(-b) + (-b)(a) + (-b)(-b)
(a - b)2 = aa - ab - ab + bb
(a - b)2 = a2 - 2ab + b2
EJEMPLO:
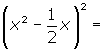
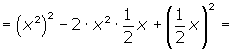
Usando la identidad: (3x2 - z)2 = (3x2)(3x2) - 2(3x2)(z) + (z)(z)
(3x2 - z)2 = 9x4 - 6x2z + z2
Ésta última expresión se utiliza con mucha frecuencia para factorizar un polinomio. Noten que factorizar la expresión  es el proceso inverso a desarrollar la expresión
es el proceso inverso a desarrollar la expresión 
El desarrollo de un un binomio al cuadrado se llama trinomio cuadrado perfecto.
a2 + 2 a b + b2 = (a + b)2
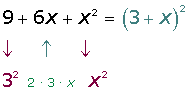
a2 − 2 a b + b2 = (a − b)2
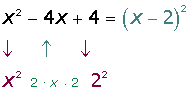
El desarrollo de un un binomio al cuadrado se llama trinomio cuadrado perfecto.
a2 + 2 a b + b2 = (a + b)2
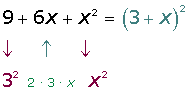
a2 − 2 a b + b2 = (a − b)2
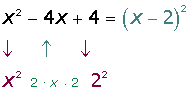


Buen aporte, bien explícito ;)
ResponderEliminarla verdad no se ni ke pedo con el blok, pero ese trabajoe sta padre..... luego ne ayudas a hacer ni blik ok
ResponderEliminarMe parece muy buena tu entrada como apoyo para aclarar ciertas dudas sobre este mismo tema pues cuando lo vimos en clase lo hicimos muy brevemente.
ResponderEliminar